This blog post is ninth in the Advent of Code 2021 series and shows a JavaScript-based solution to the problem described in Day 9.
All solutions are in this GitHub repository.
Solving Part One
The goal of part one is to find the low points of the given matrix of heights. Then we must calculate the risk level by summing the heights of low points and adding 1 for each low point.
We can break down the solution as follows:
- read the input into a matrix
- traverse the matrix
- check if a height is a low point by comparing it to each neighbour
- calculate the risk level
Storing elements into a matrix is a good choice since the problem requires checking neighbouring elements. The split function adds the data into rows and columns. The parseInt function converts each digit from a string to a number.
const heightMatrix = data
.split('\n')
.map((row) => row.split('').map((height) => parseInt(height)))
Traverse the matrix
We can traverse the matrix using nested for loops or forEach functions.
heightMatrix.forEach((row, i) => {
row.forEach((height, j) => {
})
})
Check if a height is a low point by comparing it to each neighbour
The following diagram illustrates the indices of the four neighbours of an element in a matrix.
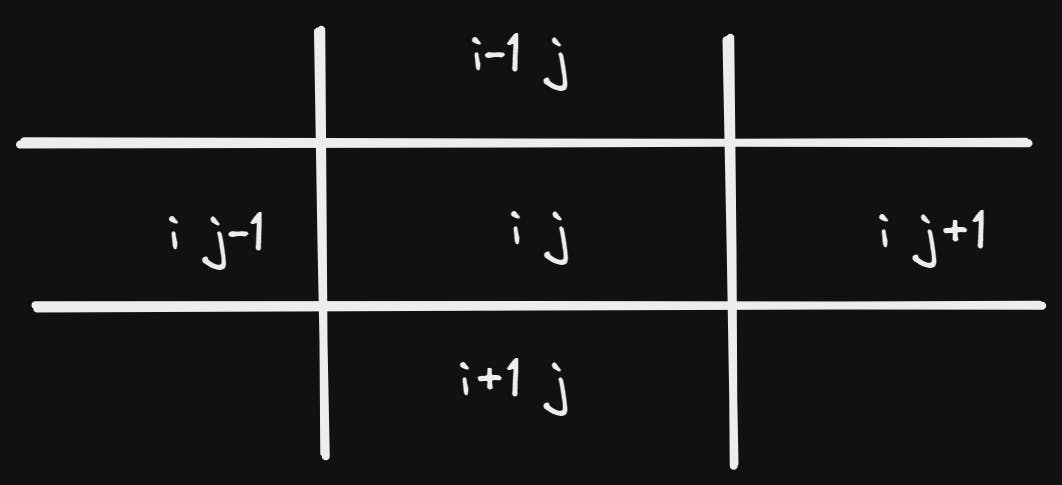We can determine if a height is a low point by comparing it to each neighbour. If it is higher or equal to any neighbouring heights, it is not a low point (return false). Otherwise, we found a low point (return true).
const isLowPoint = (matrix, i, j) => {
if (matrix[i][j] >= matrix[i - 1][j]) {
return false
}
if (matrix[i][j] >= matrix[i + 1][j]) {
return false
}
if (matrix[i][j] >= matrix[i][j - 1]) {
return false
}
if (matrix[i][j] >= matrix[i][j + 1]) {
return false
}
return true
}
The algorithm, however, does not account for elements on the edge of the matrix. Consider the number of rows and columns defined according to the height matrix lengths:
const rows = heightMatrix.length
const cols = heightMatrix[0].length
Elements on the edge of the matrix don't have all neighbours, so we must add the following rules:
- on the first row
i === 0, so we should not check the top neighbour i - 1 unless i - 1 >= 0
- on the last row
i === rows - 1, so we should not check the bottom neighbour i + 1 unless i + 1 < rows
- on the first column
j === 0, so we should not check the left neighbour j - 1 unless j- 1 >= 0
- on the last column
j === cols - 1, so we should not check the right neighbour j + 1 unless j + 1 < cols
So, we can rewrite the checks of the isLowPoint function as follows:
const isLowPoint = (matrix, rows, cols, i, j) => {
if (i - 1 >= 0 && matrix[i][j] >= matrix[i - 1][j]) {
return false
}
if (i + 1 < rows && matrix[i][j] >= matrix[i + 1][j]) {
return false
}
if (j - 1 >= 0 && matrix[i][j] >= matrix[i][j - 1]) {
return false
}
if (j + 1 < cols && matrix[i][j] >= matrix[i][j + 1]) {
return false
}
return true
}
Calculate the risk level
Finally, we can calculate the risk level by adding each newly found low point height and incrementing the total risk level by 1.
let riskLevel = 0
heightMatrix.forEach((row, i) => {
row.forEach((height, j) => {
if (isLowPoint(heightMatrix, rows, cols, i, j)) {
riskLevel += 1 + height
}
})
})
The final solution for part one is in my GitHub repository.
Solving Part Two
The goal of part two is to calculate the size of each basin surrounding a low point. Basins are a group of neighbouring heights delimited by heights of 9 since 9 is not part of any basin. We need to multiply the three largest basin sizes to solve the challenge.
I wrote a solution using the following top-down approach:
- add basin size for each low point into an array
- sort the array to find and multiply the three largest basin sizes
- create a binary basin map
- calculate basin size based on binary basin map
- mark basin map recursively
Add basin size for each low point into an array
I adjusted the solution from part one to calculate and add basin size to an array whenever we find a low point.
const basinSizes = []
heightMatrix.forEach((row, i) => {
row.forEach((height, j) => {
if (isLowPoint(heightMatrix, rows, cols, i, j)) {
basinSizes.push(findBasinSize(heightMatrix, rows, cols, i, j))
}
})
})
We can then outline the findBasinSize function like so:
const findBasinSize = (matrix, rows, cols, i, j) => {
const basinMap = initializeBasinMap(rows, cols)
markBasin(matrix, basinMap, rows, cols, i, j)
return calculateBasinSize(basinMap)
}
Sort the array to find and multiply the three largest basin sizes
We can sort the array of basin sizes in descending order to find the three largest sizes. We can then return the product of those sizes.
basinSizes.sort((a, b) => b - a)
return basinSizes[0] * basinSizes[1] * basinSizes[2]
Create a binary basin map
The binary basin map is a matrix of the same size as the height matrix. We initialize each element with 0 and mark the ones belonging to the basin with 1.
const initializeBasinMap = (rows, cols) => {
const basinMap = new Array(rows)
for (let k = 0; k < rows; k++) {
basinMap[k] = new Array(cols).fill(0)
}
return basinMap
}
Mark basin map recursively
We can write a recursive algorithm that starts from the low point, marks it on the basin map, then traverses all neighbours and marks them on the basin map. The recursion stop condition is when reaching an element with height 9 or an element already marked on the map.
const markBasin = (matrix, basinMap, rows, cols, i, j) => {
if (matrix[i][j] === 9 || basinMap[i][j] === 1) {
return
}
basinMap[i][j] = 1
if (i - 1 >= 0) {
markBasin(matrix, basinMap, rows, cols, i - 1, j)
}
if (i + 1 < rows) {
markBasin(matrix, basinMap, rows, cols, i + 1, j)
}
if (j - 1 >= 0) {
markBasin(matrix, basinMap, rows, cols, i, j - 1)
}
if (j + 1 < cols) {
markBasin(matrix, basinMap, rows, cols, i, j + 1)
}
}
The first call contains the low point indices
markBasin(matrix, basinMap, rows, cols, i, j)
Calculate basin size based on binary basin map
Once we have marked each height belonging to the current basin map, we can sum all the basin map values to find the basin's size.
const calculateBasinSize = (basinMap) => {
let size = 0
basinMap.forEach((row) => {
row.forEach((value) => {
size += value
})
})
return size
}
The final solution for part two is in my GitHub repository.
Conclusion
Day 9 was about traversing a matrix of heights, finding low points by comparing each element to its neighbours in the matrix and recursively finding a basin of adjacent heights.
